February Product Update: More Accuracy, More Control in AI Data Labeling
How new annotation tools and access controls are improving precision from geospatial mapping to enterprise workflows
Learn the latest techniques to building high-quality datasets for better performing AI.
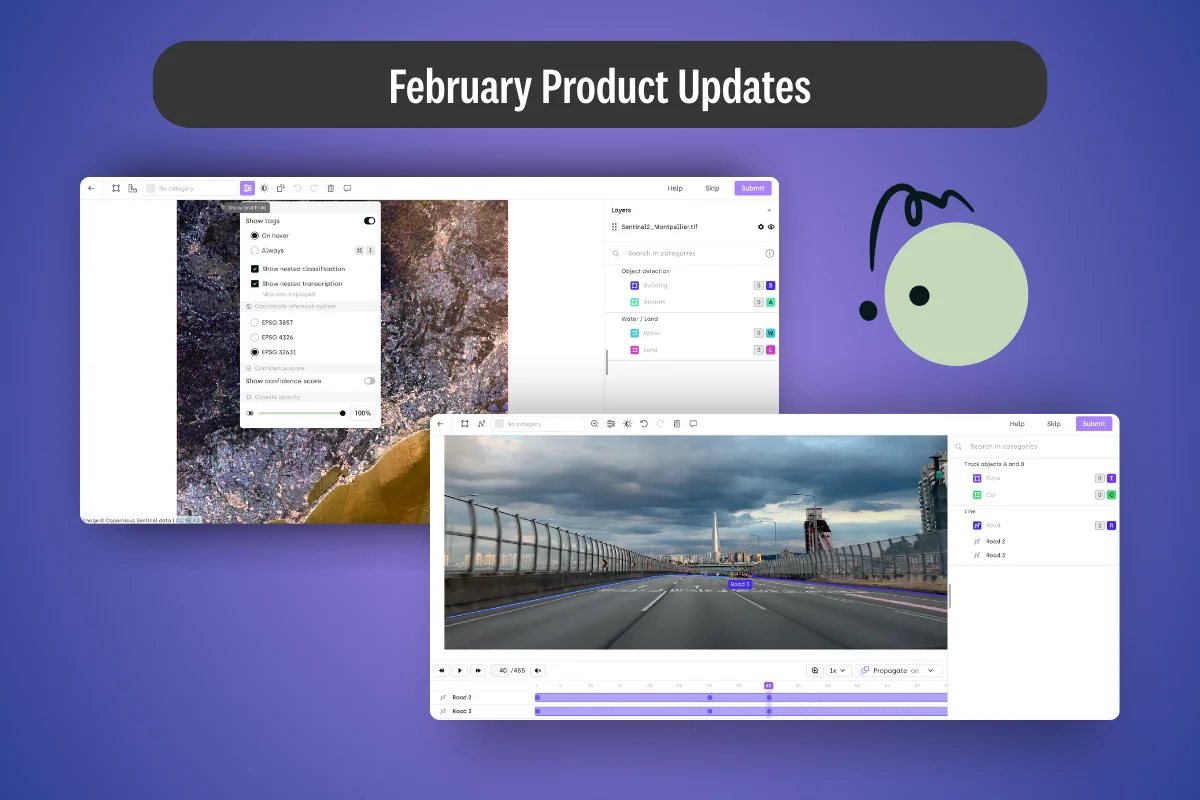
How new annotation tools and access controls are improving precision from geospatial mapping to enterprise workflows
.png)
.webp)
LLM-as-a-judge and HITL aren’t competing approaches — they’re complementary layers. This article covers the practical keys to making both work together reliably in enterprise AI systems.
.png)
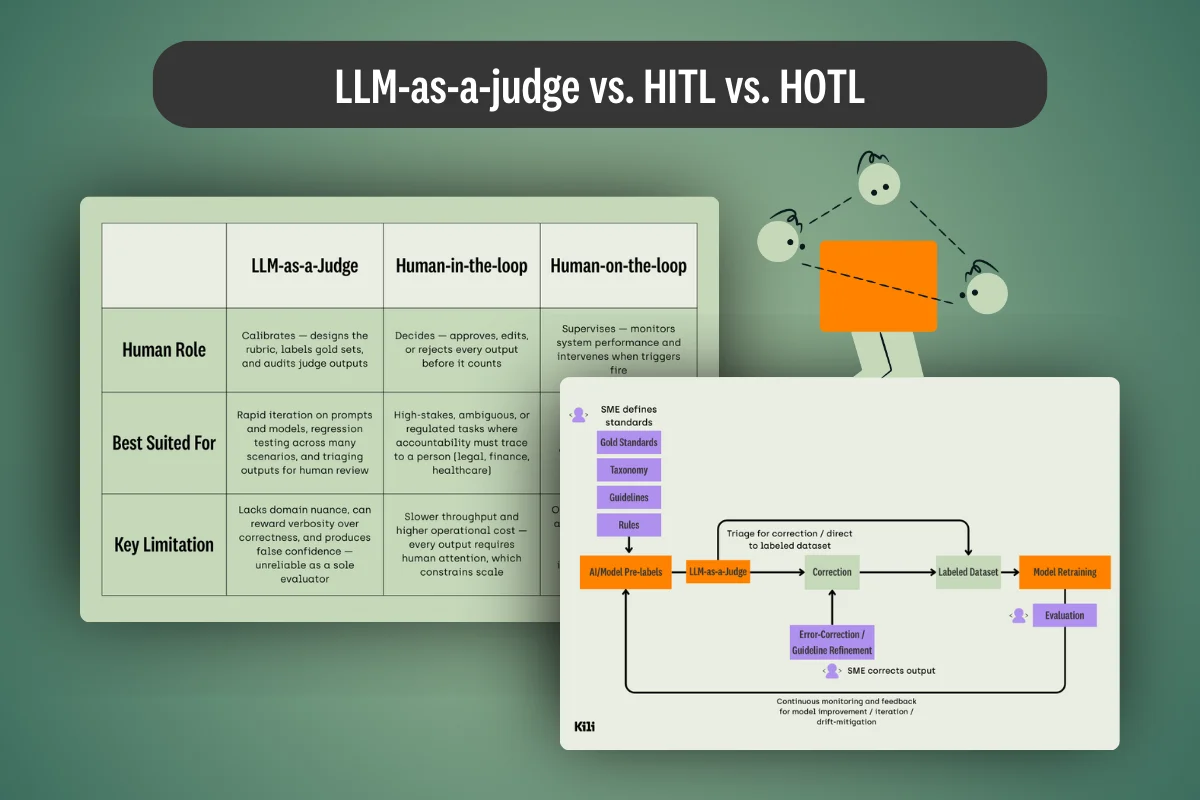
What's the difference between LLM-as-a-judge, HITL, and HOTL workflows? We cover this and provide practical tips for each application in our latest guide.
.png)

How new annotation tools are transforming workflows from electronics inspection to agricultural monitoring
.png)
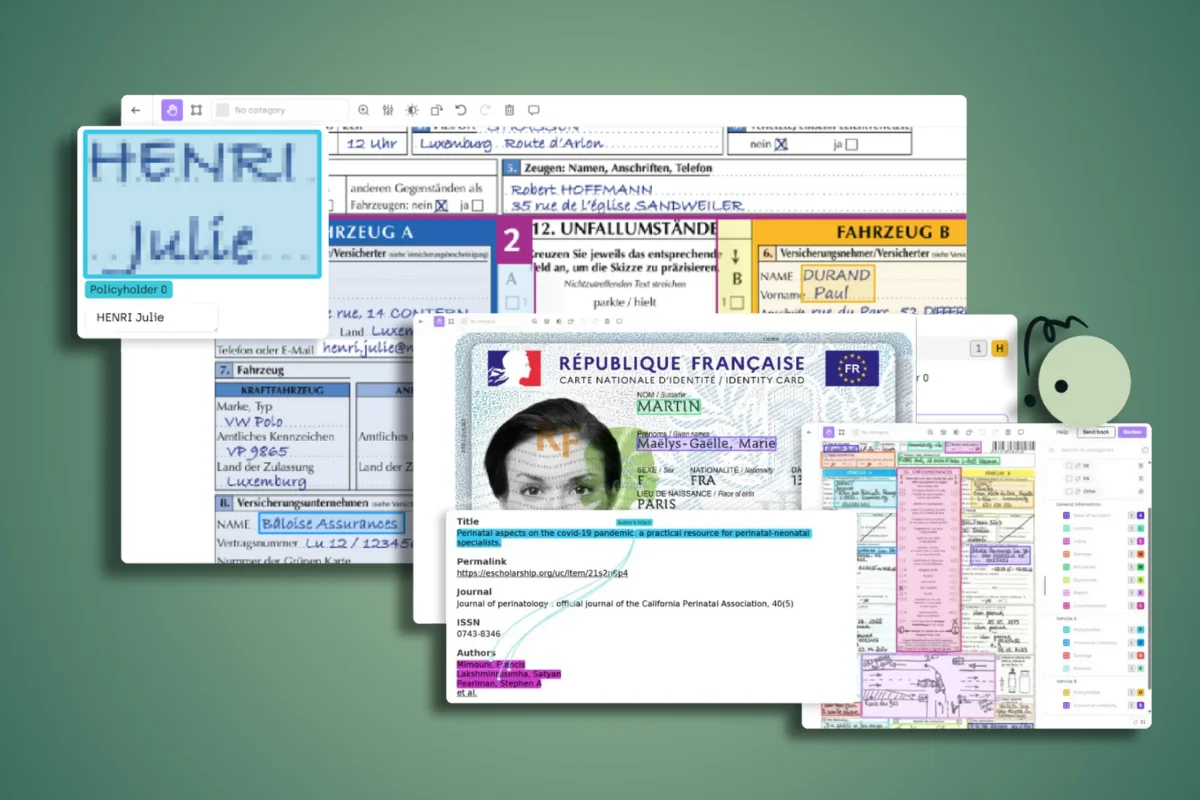
This guide will walk you through everything you need to know about OCR data labeling, from understanding the fundamentals to implementing quality workflows that scale across your organization.
.png)

Explore the FineWeb2 dataset: 20TB of multilingual pre-training data covering 1,000+ languages. Learn how its filtering pipeline builds better LLMs.
.png)

Intelligent Document Processing (IDP) minimises human errors by automating data entry. Learn more about what IDP is, how it works and its benefits for modern enterprises.
.png)