Mean Average Precision (mAP): definition
The mAP is a metric used to measure the performance of a model that focuses on object detection tasks and information retrieval on images. The mAP leverages the following sub-metrics:
- 1. Confusion Matrix
- 2. Intersection over Union(IoU)
- 3. Precision
- 4. Recall
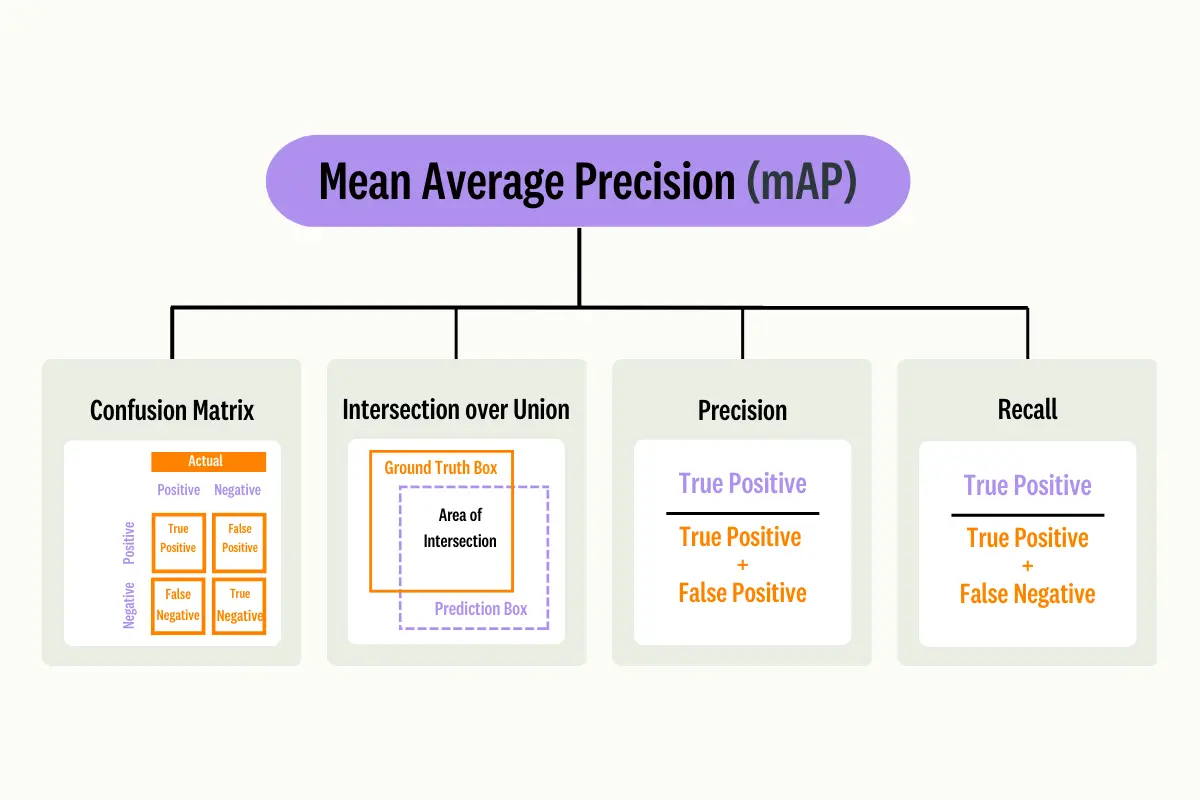
Mean Average Precision (mAP)
You'll find their definitions below.
Confusion Matrix
For a given class, the Confusion Matrix requires the following 4 components:
- True Positive - The predicted label is equal to the class and the ground truth label is equal to the class.
- True Negative - The predicted label is the class while the ground truth label is not the class.
- False Positive - The predicted label is the class and the ground truth is not the class (Type I Error).
- False Negative - The predicted label is not the class and the ground truth label is the classType II Error).
Intersection over Union (IoU)
Intersection over Union (IoU) is used to measure the accuracy of the localization provided by an object detector on a particular dataset. It does this by using the ground truth box and measures how much the predicted bounding box coordinates overlap the ground truth box coordinates.
Precision measures the quality of your model by its ability to find True Positives out of all positive predictions.
Recall
Whereas, Recall is about quantity and measures your model's ability to be able to find true positives out of all predictions.
mAP is a well-known performance metric that is frequently used to evaluate machine learning models. The metric is the most popular with benchmark challenges such as COCO, ImageNET challenge, Google Open Image Challenge, etc.
It is used in many tasks, some of which we’ve discussed, such as object detection algorithms and information retrieval tasks, but it is also used in segmentation systems, search engine evaluation, and in measuring the overall effectiveness of search algorithms.
When improving your machine learning model, you sometimes need a single-number metric. This is what mAP provides. The metric helps us obtain the average AP over all detected classes.
Precision-Recall Curve 101
When it comes to mAP, there is a trade-off between precision and recall. They both consider false positives (FP) and false negatives (FN), making mAP a suitable metric for most detection applications.
The Precision-Recall curve is a plot of the precision on the y-axis, and the recall on the x-axis for different thresholds. The curve summarizes the trade-off between the true positive rate and the positive predictive value for a predictive model.
Precision, also referred to as the positive predictive value, describes how well a model predicts the positive class.
Recall, also called sensitivity tells you if your model made the right predictions when it should have.
So why do we need the Precision-Recall curve rather than just using Precision and Recall independently? This is all because of the trade-off that the curve provides, allowing you to maximize the effects of both Precision and Recall.
The trade-off between the two metrics is essential, as working independently can cause issues in the model's performance. For example, if a model has a high recall value but a low precision value, it means that the model is classifying as many negative samples as it is positive samples. If a model has a high precision value, but a low recall value, it means that the model has the ability to classify samples as positive, but only some.
Therefore, the Precision-Recall curve allows you to select the threshold to get the best compromise between these metrics. In order to create this curve, you will need the ground-truth labels, the prediction scores of the samples, and a variety of thresholds in order to convert the prediction scores into class labels.

Precision-Recall Curve Representation
How to Compute Mean Average Precision
The mean Average Precision uses the ground-truth bounding box, compares it to the detected box, and returns a score. The higher the mAP score, the more accurate the model detects and makes correct predictions.
Compute Mean Average Precision
It is calculated by finding the Average Precision (AP) for each class and then the average over several classes. To calculate the AP, you will need to follow these steps:
- 1. Generate the prediction scores.
- 2. Convert the prediction scores into class labels
- 3. Calculate the 4 attributes of the confusion matrix
- 4. Calculate the precision and recall metrics.
- 5. Calculate the area under the precision-recall curve.
- 6. Measure the average precision.
The formula for mAP essentially tells us that, for a given class, k, we need to calculate its corresponding AP. The mean of these collated AP scores will produce the mAP and inform us how well the model performs. To understand how this works, I will explain the meaning of precision at K.

Mean Average Precision (mAP) formula
The concept of precision at K used in the calculation of mAP (AP @ K) stands for the Mean Average Precision at K. It is used to evaluate if the predicted items are relevant and if the most relevant items are at the top. The number of correctly labeled predicted labels is calculated, where K represents the top K labels that are considered.
Therefore, the Average Precision at K is the sum of the precision at K of the values of K divided by the total number of relevant items in the top K results. If we were to calculate the mean average precision at K, we measure the Average Precision at K averaged over all queries (entire dataset).
How to Improve the Mean Average Precision of a model
When working with models, you will always want to find ways to improve your metric score. This can be done using several means: by working on data quality, optimizing the algorithm, or improving the annotation process.

Three elements to consider to improve the mean Average Precision (mAP)
Data Quality
Increasing the quality of your training data is imperative to a machine learning model’s performance. Quality data means data that it is representative of the data that will be found when the model is deployed in production: the image attributes should be similar (brightness, contrast, zoom level, …), should contain the same background elements, and all the objects you want to detect are present in multiple and diverse instances in the training data.
.webp)
Example of a Precision-Recall curve
Optimizing the object detection algorithm
The state-of-the-art object detection algorithms, such as Convolutional Neural Networks Fast R-CNN, and YOLO (You Only Look Once) are becoming more and more popular and keep improving. They have been rapidly evolving in the field of computer vision with their goal remaining the same: determining where objects are located in a given image (object localization) and which category each of these objects belongs to (object classification).
If you primarily focus on working with real-time object detection, you will typically be using YOLO-type algorithms, as shown in this Real-Time Object Detection leaderboard. The TOP 3 models are:
- 1.YOLOv7-E6E(1280)
- 1.YOLO
- 1.YOLOX
However, if your focus and aim is not constrained by real-time object detection, the best Mean Average Precision will be obtained by these algorithms:
- 1. InternImage-DCNv3-H
- 2. Cascade Eff-B7 NAS-FPN
- 3. RF-ConvNeXt-T Cascade R-CNN
Improving the annotation process
Data annotations are typically manual tasks that become tedious over time. Especially when the dataset becomes more complex and large, there’s a lot of room for error. To prevent this from happening, you can follow these strategies:
- Ensure your annotation instructions are user-friendly but comprehensive.
- Ensure that the annotators have been quality-screened.
- Add a review and evaluation stage to ensure the benchmark is met.
Mean Average Precision in Practice: Object Detection
Let’s put it into practice, referring to the steps in the computing Mean Average Precision section.
- 1. Generate the prediction scores.
- 2. Convert the prediction scores into class labels.
- 3. Calculate the 4 attributes of the confusion matrix
- 4. Calculate the precision and recall metrics.
- 5. Calculate the area under the precision-recall curve.
- 6. Measure the average precision.
Steps 1 and 2 generate the prediction scores and convert them into class labels.
First, we need to generate the prediction scores and then convert them into class labels.
In order to convert the predicted scores into a class label, a threshold is required. If the predicted score is equal to or more than the threshold, the sample is classified as one class. If not, it will be classified as the other class.
If we agree that we have a threshold of 0.5 if the score is above or equal to the threshold, it is Positive; otherwise, it is Negative.
import numpy
pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3]
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive"]
threshold = 0.5
y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]
print(y_pred)Output:
This is the output for the class labels.
['positive', 'negative', 'positive', 'positive', 'positive', 'positive', 'negative', 'negative', 'negative', 'negative']Steps 3 and 4 - Calculate confusion matrix, precision, and recall
We have the ground truth and predicted labels available in the y_true and y_pred variables. The next step is to calculate the 4 attributes of the confusion matrix, precision, and recall:
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
r = numpy.flip(confusion_matrix(y_true, y_pred))
print('confusion matrix:')
print(r)
precision = precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(f"precision: {precision}")
recall = recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(f"recall: {recall}")Output:
confusion matrix:
[[4 2]
[1 3]]
precision: 0.8
recall: 0.6666666666666666Step 5 - Calculate area under the precision-recall curve
We now need to calculate the area under the precision-recall curve. This curve will help select the best threshold to maximize both precision and recall metrics.
In order to calculate the area under the curve, we need the ground-truth labels, the prediction scores of the samples, and some thresholds to convert the prediction scores into class labels.
# ground truth labels
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive", "positive", "positive", "positive", "negative", "negative", "negative"]
# prediction scores
pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3, 0.7, 0.5, 0.8, 0.2, 0.3, 0.35]
# thresholds
thresholds = numpy.arange(start=0.2, stop=0.7, step=0.05)Output of thresholds:
confusion matrix:
[[4 2]
[1 3]]
precision: 0.8
recall: 0.6666666666666666We need to create a function called precision_recall_curve() which accepts the ground-truth labels, prediction scores, and thresholds. It will return two lists, one for the precision values and one for the recall values.
def precision_recall_curve(y_true, pred_scores, thresholds):
precisions = []
recalls = []
for threshold in thresholds:
y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]
precision = precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
recall = recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
precisions.append(precision)
recalls.append(recall)
return precisions, recalls
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive", "positive", "positive", "positive", "negative", "negative", "negative"]
pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3, 0.7, 0.5, 0.8, 0.2, 0.3, 0.35]
thresholds=numpy.arange(start=0.2, stop=0.7, step=0.05)
precisions, recalls = precision_recall_curve(y_true=y_true, pred_scores=pred_scores,thresholds=thresholds)Using matplotlib, you can plot the precision-recall curve.
Output:
import matplotlib.pyplot as plt
plt.plot(recalls, precisions, linewidth=4, color="red")
plt.xlabel("Recall", fontsize=12, fontweight='bold')
plt.ylabel("Precision", fontsize=12, fontweight='bold')
plt.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
plt.show()Step 6 - Calculate Average Precision
The last step is to calculate the Average Precision in order to summarize the precision-recall curve into a single value that represents the average of all precisions.
precisions.append(1)
recalls.append(0)
precisions = numpy.array(precisions)
recalls = numpy.array(recalls)
AP = numpy.sum((recalls[:-1] - recalls[1:]) * precisions[:-1])
print(AP)Output:
0.8898809523809523The closer the average precision is to 1, the better, as it indicates a perfect model.
Mean Average Precision (mAP): Key Takeaways
- Mean Average Precision is a metric used to measure the performance of a model for tasks such as object detection tasks and information retrieval.
- mAP leverages these sub-metrics: Confused Matrix, Intersection over Union(IoU), Recall, and Precision.
- The Precision-Recall curve allows you to select the threshold to get the best compromise between the two metrics.
- 3 ways you can improve your mAP output are by improving your data quality, optimizing the algorithm, and improving the annotation process.

.png)
_logo%201.svg)


.webp)